Percentiles:
Dans un ensemble d’observations, la valeur en dessous de laquelle se trouve un pourcentage donné d’observations est appelée le percentile. Par exemple, le 90e percentile est la valeur en dessous de laquelle se situent 90 % des observations de l’ensemble de données. Il s’agit d’un compteur essentiel dans les scénarios où des valeurs aberrantes (des valeurs de temps de réponse excessivement élevées dans le cas de résultats de performance) sont trouvées et ont un impact sur le temps de réponse moyen de la transaction. Eg. Si, pour une transaction, le temps de réponse est de 1 seconde pour 99 transactions et de 100 secondes pour la 100e transaction. Le temps de réponse moyen est alors de 2 secondes, mais le temps de réponse du percentile 90 est de 1 seconde. Ainsi, le percentile néglige l’effet des valeurs aberrantes observé dans le cas des moyennes.
Valeurs normales :
Les valeurs normales sont les valeurs de l’ensemble de données qui se répètent le plus grand nombre de fois dans l’ensemble de données. Il peut également être défini comme le nombre de l’ensemble de données qui se répète le plus fréquemment.
Par exemple, supposons que nous ayons l’ensemble de données suivant –
19, 3, 3, 88, 21, 21, 88, 19, 19, 19
Dans cet ensemble de données, 15 apparaît quatre fois, 21 deux fois, 88 deux fois et 3 deux fois. Le mode de cet ensemble d’observations est donc 19.
Moyennes :
La moyenne n’est rien d’autre que la moyenne de tous les chiffres de l’ensemble des observations. Il suffit d’additionner tous les points de données et de diviser le total par le nombre de points de données de l’ensemble. Par exemple, la moyenne de 3, 4 et 5 est de 4.
Les médians:
Médiane signifie valeur moyenne. Lorsque tous les nombres de la liste sont classés par ordre croissant ou décroissant, le nombre qui se trouve au milieu est appelé la médiane de l’ensemble d’observations. En cas de nombre pair de valeurs dans l’ensemble d’observation, la moyenne des deux nombres du milieu est la médiane de l’ensemble d’observation.
Par exemple, supposons que nous ayons l’ensemble de données suivant –
19, 3, 3, 88, 21, 21, 88, 19, 19, 19
Dans l’ordre croissant, l’ensemble de données peut être écrit comme suit : –
3, 3, 19, 19, 19, 19, 21, 21, 88, 88
Dans cet exemple, la médiane est la moyenne de deux 19 qui sont les valeurs moyennes de cette série. La médiane est donc de 19.
Écarts types:
L’écart-type permet de comprendre la dispersion ou la variation de tous les éléments de données par rapport à la moyenne de l’ensemble de données. Un écart-type plus élevé signifie que les points de données sont très dispersés et un écart-type plus faible indique que les points sont proches de la moyenne de l’ensemble des données.
Pour un ensemble fini de nombres, l’écart-type est calculé en prenant la racine carrée de la moyenne des différences au carré des valeurs par rapport à leur valeur moyenne. Par exemple, pour un ensemble de données comprenant les 8 valeurs suivantes, l’écart-type peut être calculé comme suit –
***Cette photo est tirée de la page Wikipedia.
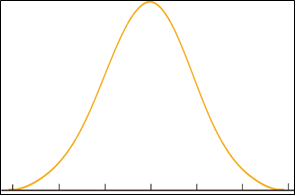Distributions normales:
La distribution la plus couramment observée dans la pratique, dans laquelle une fonction de probabilité de distribution continue est suivie. Dans cette distribution, les ensembles de données sont pondérés en fonction du centre (ou de la valeur médiane) de la distribution. Une distribution normale suit la courbe en cloche (collée à côté). Plus la distribution est petite, plus la courbe en cloche est haute.
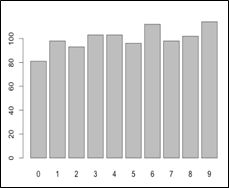Distributions uniformes:
Un ensemble de nombres aléatoires régulièrement espacés entre les bornes supérieure et inférieure est dit suivre une distribution uniforme. Dans le cas d’une distribution uniforme, chaque nombre de l’ensemble de données devrait apparaître à peu près le même nombre de fois.
Les valeurs aberrantes:
Tout point de données qui se situe au-delà de 3 écarts types ou de la valeur du percentile 99 pour un ensemble de données est une valeur aberrante pour cet ensemble de données. Dans le cas des tests de performance, les valeurs aberrantes sont des pics soudains observés dans les tests, qui peuvent être dus à de nombreuses raisons inattendues. Les personnes travaillant dans ce domaine ont tendance à ignorer ces transactions ; cependant, je suggérerais de procéder à une brève analyse des raisons pour lesquelles la valeur aberrante a été observée avant de l’ignorer complètement. Cela peut vous aider à identifier un problème de performance.
Intervalles de confiance:
Il s’agit d’un indicateur utilisé pour mettre en évidence la fiabilité d’une estimation. Il s’agit de la probabilité qu’une valeur se situe entre une limite supérieure et une limite inférieure d’une distribution de probabilité. Un intervalle de confiance à 95 % pour le logarithme du rapport de cotes est obtenu par 1,96 erreur standard de part et d’autre de l’estimation.
